Objectives
In this post, we try to understand entity embedding applied to categorical variable. Entity embeddings is a way to represent a categorical variable in a new dimension. It was (and still is) mostly used in natural language processing application, to interpret a word within his context (using surrounding word). But now, it is used for any categorical variable. I saw the idea (to apply embedding to categorical) while studying the fast.ai MOOC with Jeremy Howard and I found the idea awesome. Since then, I use this idea in a few project, but didn't take the time to plot and study the embedding created in a model.
in the following example, I will use an old model that I created few months ago to predict the price of a flat (you can find the app using the model here). I will create a neural net to predict the price, with embedding for location (french department) only. Then, I will plot the embedding to see what is created by the model.
Why ?
Why entity embedding can be useful for categorical variable:
- Reduce memory usage and speeds up neural net compared to one-hot encoding (dimensionality is reduced, depending on the choosen size of the embeddings).
- Can help to generalize better (especially for high cardinality.
- Embedding vectors can be reused (but are trained depending on a specific target).
- Can reveal property of the variable (similar value will have close vector values).
Method
I won't explain the technicality behind embedding, because you can find it almost anywhere on the internet, explained by people way better than me. You can look at post that explain word2vec and if you want to understand specific applications to categorical variables, you can look at the paper written by Cheng Guo and Felix Berkhahn "Entity Embeddings of Categorical Variables". I think it is the first known application of entity embeddings for categorical variable, they used it for a Kaggle competition and won the third place.
Dimension of entity embeddings: it can be difficult to find the best size of embeddings. Most of the time, we will use trial and error, but Jeremy Howard propose the following rule of thumb for that matter: embedding size = min(50, number of categories/2). You can find this rule of thumb in the excellent fast.ai MOOC "Deep learning for coders".
Code
I use the following code (associated with custom transformers than you can find on my github):
# -*- coding: utf-8 -*-
"""
Created on Sun May 20 09:55:14 2018
@author: thibault
"""
import pandas as pd
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense, Dropout, Input, Reshape, Embedding, concatenate
from keras import regularizers
from keras.models import Model
from sklearn.decomposition import PCA
import sys
PATH = "/home/thibault/Documents/Flask_logement/"
PATH_DATA = PATH + "Data/"
PATH_FUNCTION = "/home/thibault/Documents/Embeddings_categorical/function/"
sys.path.append(PATH_FUNCTION)
import custom_transformers
X_COLUMNS = ['typedebien', 'typedetransaction', 'surface', 'nb_photos', 'si_sdEau', 'si_sdbain',
'si_balcon', 'naturebien', 'idtypecuisine', 'idtypecommerce',
'idtypechauffage', 'etage', 'nb_chambres', 'nb_pieces', 'departement']
Y_COLUMN = ["prix"]
X_CATEGORICAL = ['typedebien', 'typedetransaction', 'si_sdEau',
'si_sdbain', 'si_balcon', 'naturebien', 'idtypecuisine',
'idtypecommerce', 'idtypechauffage', 'departement']
X_CONTINUOUS = ['surface', 'nb_photos', 'etage', 'nb_chambres', 'nb_pieces']
EMBEDDING = True # Boolean to decide if we launch model with or without embeddings
def prepare_columns(data, X_COLUMNS, Y_COLUMN):
data.loc[:, "departement"] =\
data.codepostal.map(lambda x: str(x)[:2])
res = data.loc[:, X_COLUMNS + Y_COLUMN]
return(res)
def handle_missing_value(data, categorical_columns, continous_columns):
data.loc[:, categorical_columns] =\
data.loc[:, categorical_columns].fillna("missing")
# fill missing continous variable with median => Not a good practise
data.loc[:, continous_columns] =\
data.loc[:, continous_columns]\
.fillna(data.loc[:, continous_columns].median())
# drop lines with missing Y
data = data.dropna()
return(data)
def encoding(data, categorical_columns):
# Label encoding
label_encoder_dict = {}
for var_cat in categorical_columns:
print("encode " + var_cat)
encoder_name = "label_encoder_" + var_cat
label_encoder_dict[encoder_name] = LabelEncoder()
data.loc[:, var_cat] =\
label_encoder_dict[encoder_name].fit_transform(data.loc[:, var_cat])
# one-hot_encoding
data_encoded =\
pd.get_dummies(data, dummy_na=True, columns=categorical_columns)
return(data_encoded)
def construct_model(embedding=False):
if embedding == False:
# Model without embeddings
model = Sequential()
model.add(Dense(50, input_dim=137, activation='relu', kernel_regularizer=regularizers.l2(0.001)))
model.add(Dropout(0.25))
model.add(Dense(25, activation='relu', kernel_regularizer=regularizers.l2(0.001)))
model.add(Dropout(0.25))
model.add(Dense(1))
model.compile(loss='mse', optimizer='adam', metrics=["mean_absolute_error"])
else:
# Model with embeddings
categorical_model = {}
# A - Embedding
n_output1 = 89
embedding_size1 = int(min(50, 89 / 2)) # rule of thumb by jeremy howards
categorical_model['input_layer'] = Input(shape=(1, ), name="input_embedding")
categorical_model['embedding'] =\
Embedding(input_dim=n_output1, output_dim=embedding_size1,
name="embedding", input_length=1)(categorical_model['input_layer'])
categorical_model['reshape'] =\
Reshape(target_shape=(embedding_size1,), name="reshape")(categorical_model['embedding'])
# B - all others variables
cont1 = Input(shape=(47,))
continuous1 =\
Dense(50, input_dim=137, activation='relu', kernel_regularizer=regularizers.l2(0.001))(cont1)
dropout_continuous1 = Dropout(.3)(continuous1)
merge = concatenate([categorical_model["reshape"]] + [dropout_continuous1])
hidden1 = Dense(50, input_dim=137, activation='relu', kernel_regularizer=regularizers.l2(0.001))(merge)
dropout1 = Dropout(.25)(hidden1)
hidden2 = Dense(25, activation='relu', kernel_regularizer=regularizers.l2(0.001))(dropout1)
dropout2 = Dropout(0.25)(hidden2)
output = Dense(1)(dropout2)
model = Model(inputs=[categorical_model["input_layer"]] + [cont1], outputs=output)
model.compile(loss='mse', optimizer='adam', metrics=["mean_absolute_error"])
return(model)
if __name__ == '__main__':
logements_data = pd.read_csv(PATH_DATA + "1_logements.csv", sep=";", encoding="utf-8")
logements_data.drop("Unnamed: 0", axis=1, inplace=True)
# feature enginerring and columns selection
logements_data = prepare_columns(logements_data, X_COLUMNS, Y_COLUMN)
# handling outlier
X_outlier_handler = custom_transformers.OutliersToNanWithSTD()
logements_data.loc[:, X_CONTINUOUS] =\
X_outlier_handler.fit_transform(logements_data.loc[:, X_CONTINUOUS])
Y_outlier_handler = custom_transformers.OutliersToNanWithSTD()
logements_data.loc[:, Y_COLUMN] =\
Y_outlier_handler.fit_transform(logements_data.loc[:, Y_COLUMN])
# Fill missing categorical
logements_data = handle_missing_value(logements_data, X_CATEGORICAL,
X_CONTINUOUS)
# one-hot_encoding
if EMBEDDING == False:
logements_data =\
encoding(logements_data, X_CATEGORICAL)
else:
logements_data =\
encoding(logements_data,
[x for x in X_CATEGORICAL if x != "departement"]) # We embed only departement
# we reorder departement with a dictionnary
dictionnary_dep = {}
labels = {}
for i, dep in enumerate(logements_data.departement.unique()):
dictionnary_dep[dep] = str(i)
labels[str(i)] = dep
logements_data.departement = logements_data.departement.map(dictionnary_dep)
# Split test and train
X_train, X_test, y_train, y_test =\
train_test_split(logements_data.drop(Y_COLUMN, axis=1),
logements_data.loc[:, Y_COLUMN],
test_size=0.33, random_state=38)
if EMBEDDING == True:
list_X_train = [X_train.departement] + [X_train.drop("departement", axis=1)]
X_train = list_X_train
list_X_test = [X_test.departement] + [X_test.drop("departement", axis=1)]
X_test = list_X_test
# standardise
X_scaler = MinMaxScaler()
X_train[1] =\
X_scaler.fit_transform(X_train[1])
X_test[1] =\
X_scaler.transform(X_test[1])
# Y_scaler = MinMaxScaler()
# y_train =\
# Y_scaler.fit_transform(y_train)
model =\
construct_model(embedding=True)
history = model.fit(X_train, y_train, epochs=125, batch_size=128, verbose=2,
validation_split=0.33)
# plot training
# summarize history for loss
plt.plot(history.history['loss'][2:]) # We drop the first occurence because of different in scale
plt.plot(history.history['val_loss'][2:])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# Evaluate final model
test_predictions = model.predict(X_test)
train_predictions = model.predict(X_train)
# test_predictions = Y_scaler.inverse_transform(test_predictions)
print("TEST MSE = " + str(mean_squared_error(y_test, test_predictions)))
print("TRAIN MSE = " + str(mean_squared_error(y_train, train_predictions)))
plt.scatter(y_test, test_predictions)
if EMBEDDING == True:
# Plot embedding
embedding_weight = model.get_layer(name="embedding").get_weights()[0]
tsne_model = TSNE(perplexity=70, n_components=2, init='pca', n_iter=2500, random_state=23)
pca = PCA(n_components=2, random_state=23)
new_values = tsne_model.fit_transform(embedding_weight)
x = []
y = []
for value in new_values:
x.append(value[0])
y.append(value[1])
plt.figure(figsize=(16, 16))
for i in range(len(x)):
plt.scatter(x[i],y[i])
plt.annotate(labels[str(i)],
xy=(x[i], y[i]),
xytext=(5, 2),
textcoords='offset points',
ha='right',
va='bottom')
plt.show()
Result
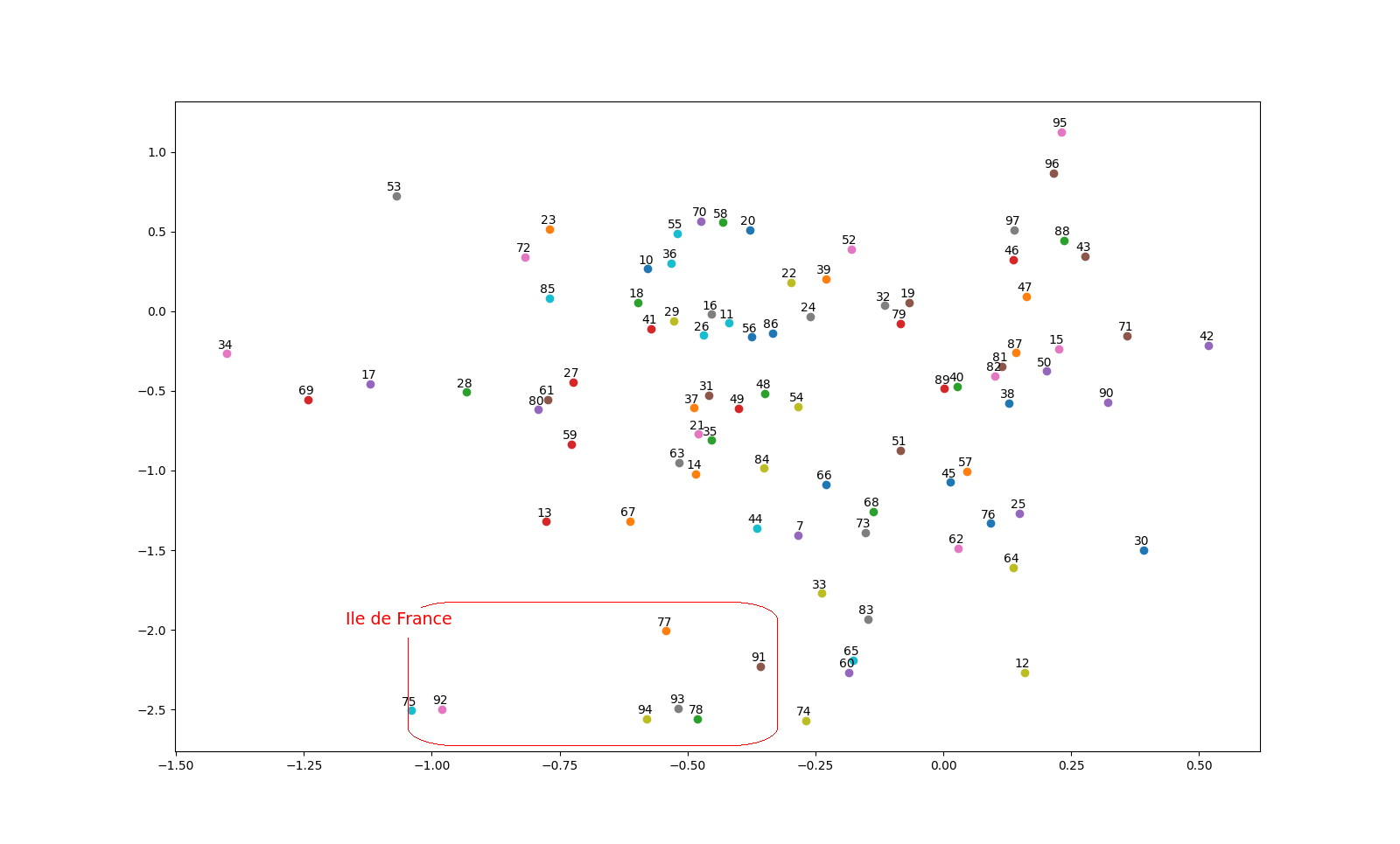
The result is interesting. We tried to plot the embeddings in two dimensions using TSNE and PCA (the previous plot is based on PCA). Because we trained the embedding with a target on renting price, we can find pattern based on price and location. For example, we can find that all the department related to "ile de France" are really close on the plot.
I was really curious to see if some pattern can be found using embedding on department, in this context. Apparently that is the case, and there is probably some other interesting pattern that I didn't notice.